Unity’s new particle system, Shuriken is a pretty versatile tool, and it’s really useful for making animations look slick.
It does have its flaws, though, as I discovered whilst attempting to make a particle tornado. Its main downfall is that it lacks a polar coordinate system and, much as polar coordinates are the bane of my student life, I have to admit they’re pretty damned useful when you’re trying to make a tornado.
I looked around the interwebs and couldn’t find any solutions to my problem that didn’t involve paying for content, so I put on my maths hat and started deriving.
Now, there are a whole bunch of spirals, but the most obvious (and, thankfully, simplest) one is the Archimedean spiral, whose “arms” are equally spaced, and it follows the basic polar formula:
$latex r=a+b\theta &s=2$
Now, that’s all well and good in polar coordinates, but we need to know it in cartesian. Not only that, but we also have to differentiate it, since Shuriken wants particle lifetime velocities, not displacements.
So
$latex x=rcos(\theta)&s=2$
and
$latex y=rsin(\theta) &s=2$
We want to differentiate that with respect to time, but we don’t have a time term. Luckily, we know that it’s rotating at a constant rate, so the angle is going to increase at a constant rate, so we can just define:
$latex theta = \lambda t &s=2$ .
Our tornado is going to increase in height at a constant rate too, so our z component of velocity is just going to be some constant that we can choose later in Unity. Meanwhile, our x and y components of velocity can be derived from our known formulae for x and y:
$latex x = (a+b\lambda t)cos(\lambda t) &s=2$
$latex v_x = (b\lambda )cos(\lambda t)-(a+b\lambda t)sin(\lambda t) &s=2$
And
$latex y = (a+b\lambda t)sin(\lambda t) &s=2$
$latex v_y = (b\lambda )sin(\lambda t)+(a+b\lambda t)cos(\lambda t) &s=2$
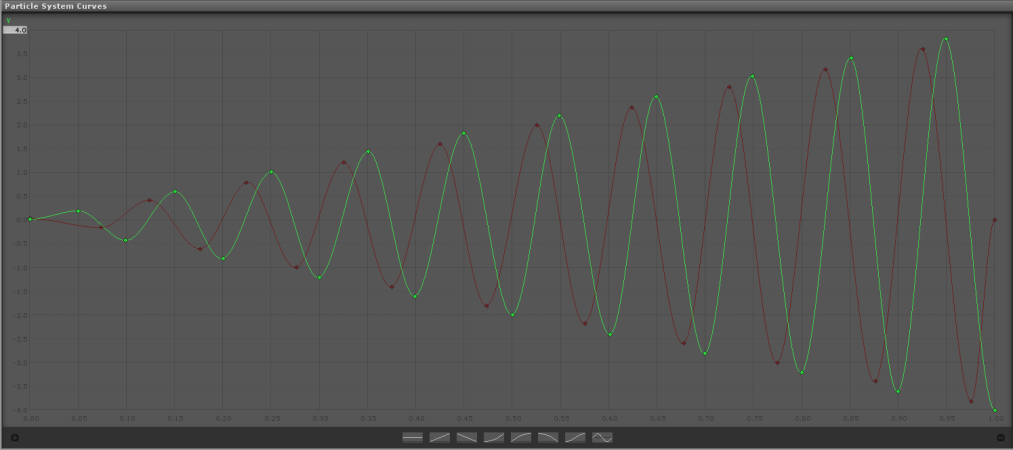
It’s all very well and good deriving that, but my feeble human brain can’t interpret a harmonic equation as something useful, and I’m sure even those more gifted of us would miss the more subtle behaviours of this equation (specific peaks, turning points etc.)
So I gave my brain a rest, arbitarily chose a, b and lambda, and threw it into MATLAB with 400 data points.
That led me to this graph:
Which I then meticulously plotted in Unity. It has a limited number of nodes, and you have to change the angles for each point so it forms a smooth curve. In short: It’s disgusting to do, and it ends up with something like this:
This is an absolute pain to plot. You have a limited number of nodes you can use, and you have tweak each one so that it ends up sinusoidal. However, if you’d rather spend 5 minutes plotting some points than paying $25 for a tornado from the asset store, this is probably your best bet.
This will form an “ideal” tornado, which doesn’t twist around randomly. For things like whirlpools and black holes, this works just great (if you have good textures and tweak the values properly), or in the case that you WANT an ideal tornado because it fits with your graphical style. However, if you’re looking for it to be more realistic, it’s pretty achieveable, but you’ll have to do a lot of messing around in the Force tab. Just set it to give a random curve between two constraining curves in x and y, and you’ll get your randomised moving tornado. It’ll also work pretty well if you set it to simulate in world space rather than local space, and have the particle system itself move around, in which case you’ll probably want a second particle system at the base making some basic dust effects.
It’s fun to note that if Unity added a polar coordinate system to Shuriken, the graph above would consist of 2 identical horizontal lines. Just slightly easier.
Here’s how it looks in the end (using Unity’s standard smoke texture, with it tweaked to different settings):
Obviously you can then tweak it however you see fit, and most importantly, texture it properly, but for now you can see the definite spiral shape.
Enjoy.